十种机器学习算法的要点
作者:探码科技, 原文链接: http://www.tanmer.com/learning/309
也许我们生活在人类历史上最关键的时期:从使用大型计算机,到个人电脑,再到现在的云计算和机器学习。机器学习现已深深的影响我们的生活!
下面我们将会为大家讲述常见机器算法名单
一.线性回归
线性回归通常用于根据连续变量估计实际数值(房价、呼叫次数、总销售额等)。我们通过拟合最佳直线来建立自变量和因变量的关系。这条最佳直线叫做回归线,并且用 Y= a *X + b 这条线性等式来表示。
理解线性回归的最好办法是回顾一下童年。假设在不问对方体重的情况下,让一个五年级的孩子按体重从轻到重的顺序对班上的同学排序,你觉得这个孩子会怎么做?他(她)很可能会目测人们的身高和体型,综合这些可见的参数来排列他们。这是现实生活中使用线性回归的例子。实际上,这个孩子发现了身高和体型与体重有一定的关系,这个关系看起来很像上面的等式。
在这个等式中:
Y:因变量
a:斜率
x:自变量
b :截距
系数 a 和 b 可以通过最小二乘法获得。
参见下例。我们找出最佳拟合直线 y=0.2811x+13.9。已知人的身高,我们可以通过这条等式求出体重。
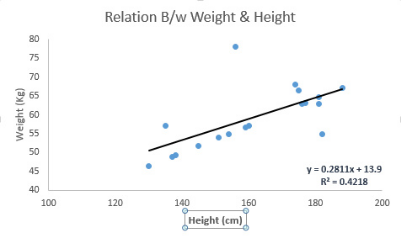
线性回归的两种主要类型是一元线性回归和多元线性回归。一元线性回归的特点是只有一个自变量。多元线性回归的特点正如其名,存在多个自变量。找最佳拟合直线的时候,你可以拟合到多项或者曲线回归。这些就被叫做多项或曲线回归。
二.决策树
根据一些 feature 进行分类,每个节点提一个问题,通过判断,将数据分为两类,再继续提问。这些问题是根据已有数据学习出来的,再投入新数据的时候,就可以根据这棵树上的问题,将数据划分到合适的叶子上。
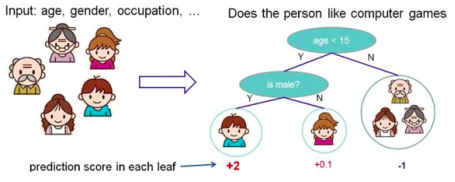
三.随机森林
在源数据中随机选取数据,组成几个子集

S 矩阵是源数据,有 1-N 条数据,A B C 是feature,最后一列C是类别
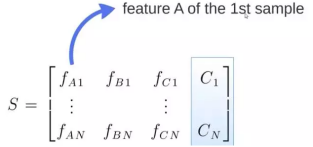
由 S 随机生成 M 个子矩阵

这 M 个子集得到 M 个决策树
将新数据投入到这 M 个树中,得到 M 个分类结果,计数看预测成哪一类的数目最多,就将此类别作为最后的预测结果
四.逻辑算法
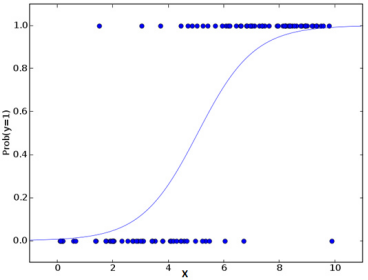
别被它的名字迷惑了!这是一个分类算法而不是一个回归算法。该算法可根据已知的一系列因变量估计离散数值(比方说二进制数值 0 或 1 ,是或否,真或假)。简单来说,它通过将数据拟合进一个逻辑函数来预估一个事件出现的概率。因此,它也被叫做逻辑回归。因为它预估的是概率,所以它的输出值大小在 0 和 1 之间(正如所预计的一样)。
让我们再次通过一个简单的例子来理解这个算法。
假设你的朋友让你解开一个谜题。这只会有两个结果:你解开了或是你没有解开。想象你要解答很多道题来找出你所擅长的主题。这个研究的结果就会像是这样:假设题目是一道十年级的三角函数题,你有 70%的可能会解开这道题。然而,若题目是个五年级的历史题,你只有30%的可能性回答正确。这就是逻辑回归能提供给你的信息。
从数学上看,在结果中,几率的对数使用的是预测变量的线性组合模型。
在上面的式子里,p 是我们感兴趣的特征出现的概率。它选用使观察样本值的可能性最大化的值作为参数,而不是通过计算误差平方和的最小值(就如一般的回归分析用到的一样)。
现在你也许要问了,为什么我们要求出对数呢?简而言之,这种方法是复制一个阶梯函数的最佳方法之一。我本可以更详细地讲述,但那就违背本篇指南的主旨了。
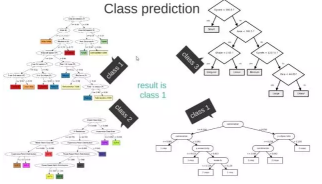
五.神经网络
Neural Networks 适合一个input可能落入至少两个类别里
NN 由若干层神经元,和它们之间的联系组成
第一层是 input 层,最后一层是 output 层
在 hidden 层 和 output 层都有自己的 classifier

input 输入到网络中,被激活,计算的分数被传递到下一层,激活后面的神经层,最后output 层的节点上的分数代表属于各类的分数,下图例子得到分类结果为 class 1
同样的 input 被传输到不同的节点上,之所以会得到不同的结果是因为各自节点有不同的weights 和 bias
这也就是 forward propagation

六.马尔可夫
Markov Chains 由 state 和 transitions 组成
栗子,根据这一句话 ‘the quick brown fox jumps over the lazy dog’,要得到 markov chain
步骤,先给每一个单词设定成一个状态,然后计算状态间转换的概率
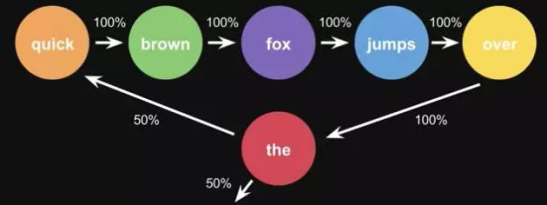
这是一句话计算出来的概率,当你用大量文本去做统计的时候,会得到更大的状态转移矩阵,例如 the 后面可以连接的单词,及相应的概率
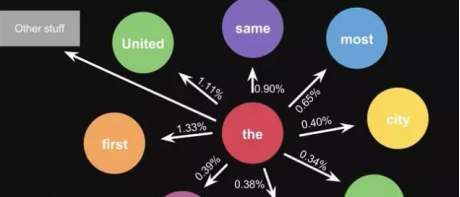
生活中,键盘输入法的备选结果也是一样的原理,模型会更高级

七.KNN(K – 最近邻算法)
该算法可用于分类问题和回归问题。然而,在业界内,K – 最近邻算法更常用于分类问题。K – 最近邻算法是一个简单的算法。它储存所有的案例,通过周围k个案例中的大多数情况划分新的案例。根据一个距离函数,新案例会被分配到它的 K 个近邻中最普遍的类别中去。
这些距离函数可以是欧式距离、曼哈顿距离、明式距离或者是汉明距离。前三个距离函数用于连续函数,第四个函数(汉明函数)则被用于分类变量。如果 K=1,新案例就直接被分到离其最近的案例所属的类别中。有时候,使用 KNN 建模时,选择 K 的取值是一个挑战。
更多信息:K – 最近邻算法入门(简化版)
我们可以很容易地在现实生活中应用到 KNN。如果想要了解一个完全陌生的人,你也许想要去找他的好朋友们或者他的圈子来获得他的信息。
在选择使用 KNN 之前,你需要考虑的事情:
- KNN 的计算成本很高。
- 变量应该先标准化(normalized),不然会被更高范围的变量偏倚。
- 在使用KNN之前,要在野值去除和噪音去除等前期处理多花功夫。
八.K 均值算法
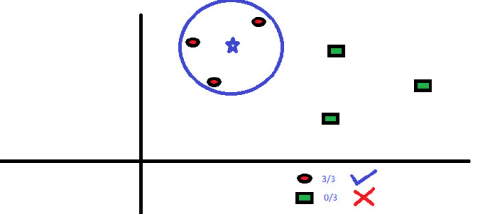
K – 均值算法是一种非监督式学习算法,它能解决聚类问题。使用 K – 均值算法来将一个数据归入一定数量的集群(假设有 k 个集群)的过程是简单的。一个集群内的数据点是均匀齐次的,并且异于别的集群。
还记得从墨水渍里找出形状的活动吗?K – 均值算法在某方面类似于这个活动。观察形状,并延伸想象来找出到底有多少种集群或者总体。

K – 均值算法怎样形成集群:
- K – 均值算法给每个集群选择k个点。这些点称作为质心。
- 每一个数据点与距离最近的质心形成一个集群,也就是 k 个集群。
- 根据现有的类别成员,找出每个类别的质心。现在我们有了新质心。
- 当我们有新质心后,重复步骤 2 和步骤 3。找到距离每个数据点最近的质心,并与新的k集群联系起来。重复这个过程,直到数据都收敛了,也就是当质心不再改变。
如何决定 K 值:
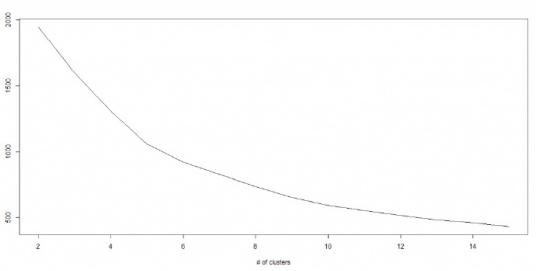
- K – 均值算法涉及到集群,每个集群有自己的质心。一个集群内的质心和各数据点之间距离的平方和形成了这个集群的平方值之和。同时,当所有集群的平方值之和加起来的时候,就组成了集群方案的平方值之和。
- 我们知道,当集群的数量增加时,K值会持续下降。但是,如果你将结果用图表来表示,你会看到距离的平方总和快速减少。到某个值 k 之后,减少的速度就大大下降了。在此,我们可以找到集群数量的最优值。
九 . EM算法
假定观测数据表示为 Y=(Y_{1},Y_{2},...,Y_{n})^{T}
未观测数据表示为Z=(Z_{1},Z_{2},...,Z_{n})^{T},则观测数据的似然函数为
P(Y|\theta )=\sum_{Z}^{ }P(Z|\theta)P(Y|Z,\theta)
通过最大似然估计建立目标函数,有
L(\theta)=logP(Y,Z|\theta )
算法1(EM算法)
输入:观测变量数据Y,隐变量数据Z,联合分布 P(Y,Z|\theta ),条件分布P(Z|Y,\theta );
输出:模型参数\theta。
1)、选择参数的初值\theta^{(0)},开始迭代;
2)、E步:记\theta^{(i)}为第i次迭代参数\theta的估计值,在第i+1次迭代的E步,计算概率分布P的期望称为Q函数
Q(\theta ,\theta ^{(i)})=E_{Z}[logP(Y,Z|\theta)|Y,\theta^{(i)}]
=\sum_{z}^{ }logP(Y,Z|\theta )P(Z|Y,\theta ^{i})
3)、M步:求使Q(\theta ,\theta ^{(i)})极大化的\theta,确定第i+1次迭代的参数估计值\theta ^{(i+1)}
\theta ^{(i+1)}=arg \underset{\theta }{max}Q(\theta ,\theta ^{(i)})
4)、重复第2)步和第3)步,直到收敛。
Z是隐随机变量,不方便直接找到参数估计。
策略:计算L(\theta )下界,求该下界的最大值;重复该过程,知道收敛到局部最大值。
下图给出EM算法的直观解释
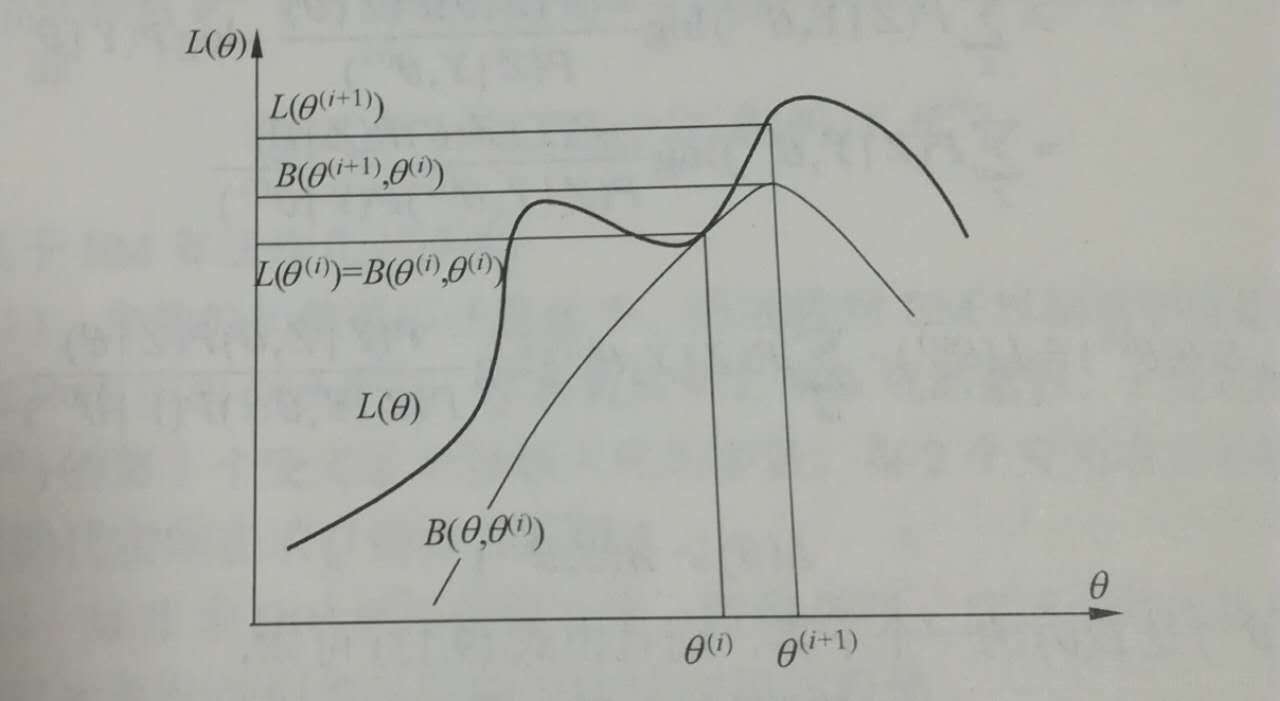
图中上方曲线为l(\theta ),下方曲线为l(\theta )的一个下界B(\theta ,\theta ^{(i)}),两个函数在点\theta =\theta ^{(i)}处相等。EM算法找到一个点\theta ^{(i+1)}使函数B(\theta ,\theta ^{(i)})极大化,也条件概率的期望函数Q极大化。EM算法在点\theta ^{(i+1)}重新计算Q函数值,进行下次迭代。在这个过程中,对数似然函数L(\theta )不断增大。从上图中可以推断出EM算法不能保证找到全局最优值。
十. 朴素贝叶斯
在预示变量间相互独立的前提下,根据贝叶斯定理可以得到朴素贝叶斯这个分类方法。用更简单的话来说,一个朴素贝叶斯分类器假设一个分类的特性与该分类的其它特性不相关。举个例子,如果一个水果又圆又红,并且直径大约是 3 英寸,那么这个水果可能会是苹果。即便这些特性互相依赖,或者依赖于别的特性的存在,朴素贝叶斯分类器还是会假设这些特性分别独立地暗示这个水果是个苹果。
朴素贝叶斯模型易于建造,且对于大型数据集非常有用。虽然简单,但是朴素贝叶斯的表现却超越了非常复杂的分类方法。
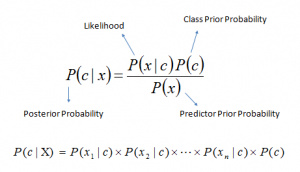
贝叶斯定理提供了一种从P(c)、P(x)和P(x|c) 计算后验概率 P(c|x) 的方法。请看以下等式:
在这里,
P(c|x) 是已知预示变量(属性)的前提下,类(目标)的后验概率
P(c) 是类的先验概率
P(x|c) 是可能性,即已知类的前提下,预示变量的概率
P(x) 是预示变量的先验概率
例子:让我们用一个例子来理解这个概念。在下面,我有一个天气的训练集和对应的目标变量“Play”。现在,我们需要根据天气情况,将会“玩”和“不玩”的参与者进行分类。让我们执行以下步骤。
步骤1:把数据集转换成频率表。
步骤2:利用类似“当Overcast可能性为0.29时,玩耍的可能性为0.64”这样的概率,创造 Likelihood 表格。
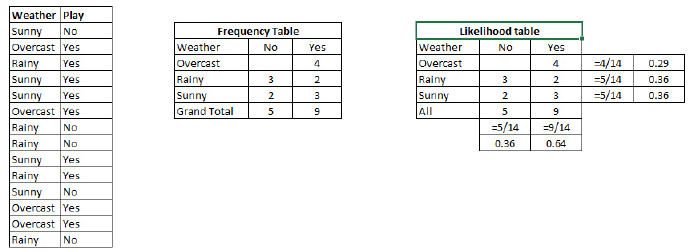
步骤3:现在,使用朴素贝叶斯等式来计算每一类的后验概率。后验概率最大的类就是预测的结果。
问题:如果天气晴朗,参与者就能玩耍。这个陈述正确吗?
我们可以使用讨论过的方法解决这个问题。于是 P(会玩 | 晴朗)= P(晴朗 | 会玩)* P(会玩)/ P (晴朗)
我们有 P (晴朗 |会玩)= 3/9 = 0.33,P(晴朗) = 5/14 = 0.36, P(会玩)= 9/14 = 0.64
现在,P(会玩 | 晴朗)= 0.33 * 0.64 / 0.36 = 0.60,有更大的概率。
朴素贝叶斯使用了一个相似的方法,通过不同属性来预测不同类别的概率。这个算法通常被用于文本分类,以及涉及到多个类的问题。